A decision tree is a non-parametric supervised learning algorithm, which is utilized for both classification and regression tasks. It has a hierarchical, tree structure, which consists of a root node, branches, internal nodes and leaf nodes.
一、ID3
1、信息熵(Information Entropy)
信息熵代表的是随机变量或整个系统的不确定性,熵越大,随机变量或系统的不确定性就越大。
例如:
一个数据集只有蓝色$\color{blue}\bullet$$\color{blue}\bullet$$\color{blue}\bullet$$\color{blue}\bullet$$\color{blue}\bullet$$\color{blue}\bullet$则它的熵很低(实际上为0)
一个数据集有蓝色绿色和红色相混合$\color{blue}\bullet$$\color{green}\bullet$$\color{green}\bullet$$\color{red}\bullet$$\color{red}\bullet$$\color{red}\bullet$,则它的熵相对较高
公式
$$E=-\displaystyle\sum_i^C p_ilog_2{(p_i)}$$
$C$:所有分类(例如颜色的种类,例如:红绿蓝)
$p_i$:在分类$i$中随机抽取一个元素的概率
举例
假设一个集合有1个蓝色,2个绿色和3个红色数据$\color{blue}\bullet$$\color{green}\bullet$$\color{green}\bullet$$\color{red}\bullet$$\color{red}\bullet$$\color{red}\bullet$,则其信息熵为:
$$\begin{align}E & = -(p_blog_2(p_b)+p_glog_2(p_g)+p_rlog_2(p_r))\\ & = -(\frac16log_2(\frac16)+\frac26log_2(\frac26)+\frac36log_2(\frac36))\\ & \approx 1.46\end{align}$$
假设一个集合只有3个蓝色数据$\color{blue}\bullet$$\color{blue}\bullet$$\color{blue}\bullet$,则其信息熵为:
$$E=-(log_21)=0$$
2、信息增益(Information Gain):
在某一条件下,随机变量不确定性减少的程度,对可取数值较多的属性有所偏好
公式
$$Gain=E_{before}-E_{split}=E_{before}-\displaystyle\sum_i^C \frac{\mid D_v\mid}{\mid D\mid}\cdot E_i$$
$\mid D\mid$:数据集样本的熵
$\mid D_v\mid$:子集中属性值为v的实例数
举例
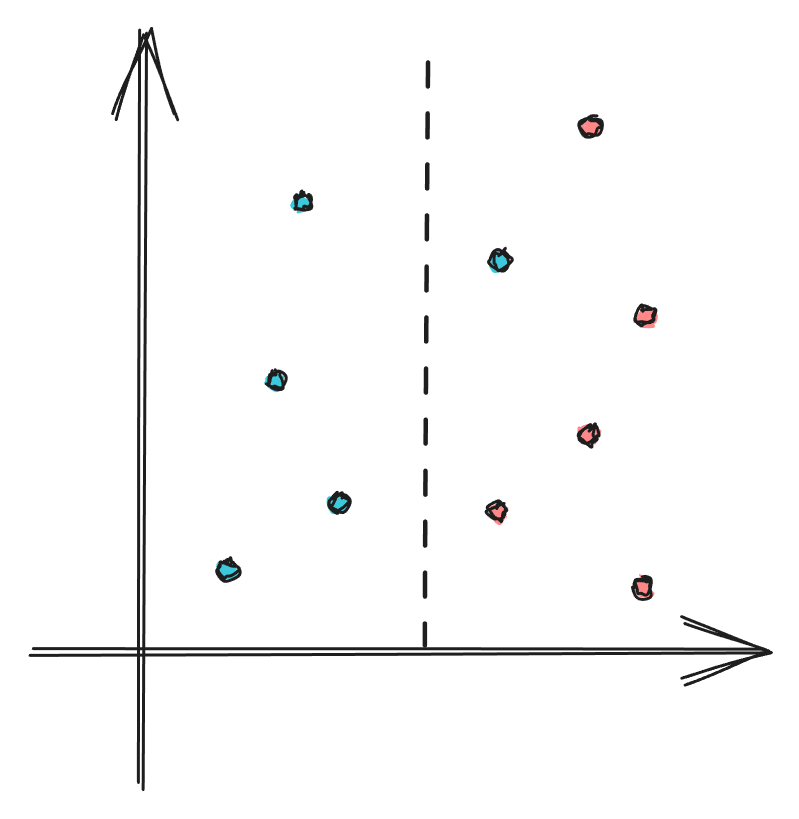
分类之前,有5个蓝色的数据和5个红色的数据,则其信息熵为:
$$E_{before}=-(\frac12log_2(\frac12)+\frac12log_2(\frac12))=1$$
分类之后,我们有两个分支,分别为左分支和右分支,则其信息熵为:
$$\begin{align}E_{left} & = -log_2(1)\\ & = 0\\E_{right} & = -(\frac16log_2(\frac16)+\frac56log_2(\frac56))\\ & \approx 0.65\end{align}$$
左侧有10个元素中的4个,因此其权重为$\frac{4}{10}$;同理右侧权重为$\frac{6}{10}$,则分类的熵为:
$$\begin{align}E_{split}&=\frac{4}{10}\cdot E_{left}+\frac{6}{10}\cdot E_{right}\\&=0.4\cdot 0+0.6\cdot 0.65\\&=0.39\end{align}$$
则信息增益Gain为:
$$Gain=1-0.39=0.61$$
二、C4.5
信息增益率(Gain Ratio)
$$Gain\_ratio=\frac{Gain}{E}=\frac{E_{before}-\displaystyle\sum_i^C \frac{\mid D_v\mid}{\mid D\mid}\cdot E_i}{-\displaystyle\sum_i^C p_ilog_2{(p_i)}}$$
三、CART(Classification and Regression Tree)
1、基尼系数(Gini Impurity)
公式
二分类:$G=p(1-p)+(1-p)(1-(1-p))=2p(1-p)$
多分类:$G=\displaystyle\sum_{i=1}^{C}p(i)\cdot(1-p(i))=1-\displaystyle\sum_{i=1}^{C}p^2(i)$
基尼系数:$Gini\_impurity=\displaystyle\sum_{i=1}^{C}\frac{\mid D_v\mid}{\mid D\mid}\cdot G_i$
基尼增益:$Gain=G_{before}-Gini\_impurity=\displaystyle\sum_{i=1}^{C}p(i)\cdot(1-p(i))-\displaystyle\sum_{i=1}^{C}\frac{\mid D_v\mid}{\mid D\mid}\cdot G_i$
完美分类举例
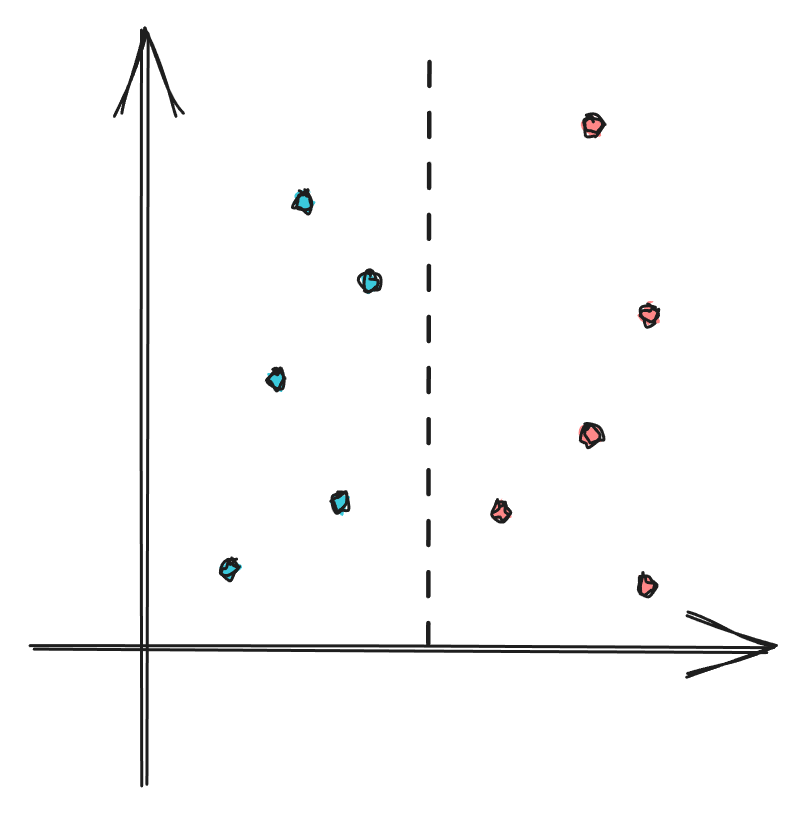
左侧全为蓝色,则其蓝色占比100%,红色占比0%,则左侧$G_{left}$为:
$$G_{left}=1\cdot (1-1)+0\cdot (1-0)=0$$
同理,右侧$G_{right}$为:
$$G_{right}=0\cdot (1-0)+1\cdot (1-1)=0$$
基系数为0是最低和最好的。只有当所有元素都是相同的类别时才能实现这一点。
不完美分类举例

未分类时,红色和蓝色各5个,占比均为50%,则$G_{before}$为:
$$G_{before}=\frac12\cdot(1-\frac12)+\frac12\cdot(1-\frac12)=0.5$$
左侧全为蓝色,则其蓝色占比100%,红色占比0%,则左侧$G_{left}$为:
$$G_{left}=1\cdot (1-1)+0\cdot (1-0)=0$$
右侧1个蓝色,占比为$\frac16$;5个红色占比为$\frac56$,则有侧$G_{right}$为:
$$\begin{align}G_{right}&=\frac16\cdot(1-\frac16)+\frac56\cdot(1-\frac56)\\&=\frac{5}{18}\\&\approx0.278\end{align}$$
基尼系数和基尼增益
$$\begin{align}Gini\_impurity&=\frac{4}{10}\cdot G_{left}+\frac{6}{10}\cdot G_{right}=0.4\cdot 0+(0.6\cdot 0.278)\approx0.167\\Gain&=G_{before}-Gini\_impurity=0.5-0.167=0.333\end{align}$$
2、回归树(Regression Tree)
公式
$$RSS=\displaystyle\sum_{j=1}^{j}\displaystyle\sum_{i \in R_j}(y_i-\widetilde{y}_{R_j})^2$$
$\widetilde{y}_{R_j}$(均值):$\widetilde{y}_{R_j}=\frac{1}{n}\displaystyle\sum_{j\in R_j}y_j$
正则化
$\displaystyle\sum_{m=1}^{\mid T\mid}\displaystyle\sum_{x_i \in R_m}(y_i-\widetilde{y}_{R_j})^2+\alpha\mid T\mid$
$\mid T\mid$:回归树叶子节点的个数
$\alpha$:可以通过交叉验证去选择
3、XGBoosting
XGBoost is a popular and efficient open-source implementation of the gradient boosted trees algorithm. Gradient boosting is a supervised learning algorithm, which attempts to accurately predict a target variable by combining the estimates of a set of simpler, weaker models.
When using gradient boosting for regression, the weak learners are regression trees, and each regression tree maps an input data point to one of its leafs that contains a continuous score. XGBoost minimizes a regularized (L1 and L2) objective function that combines a convex loss function (based on the difference between the predicted and target outputs) and a penalty term for model complexity (in other words, the regression tree functions). The training proceeds iteratively, adding new trees that predict the residuals or errors of prior trees that are then combined with previous trees to make the final prediction. It's called gradient boosting because it uses a gradient descent algorithm to minimize the loss when adding new models.
Below is a brief illustration on how gradient tree boosting works.
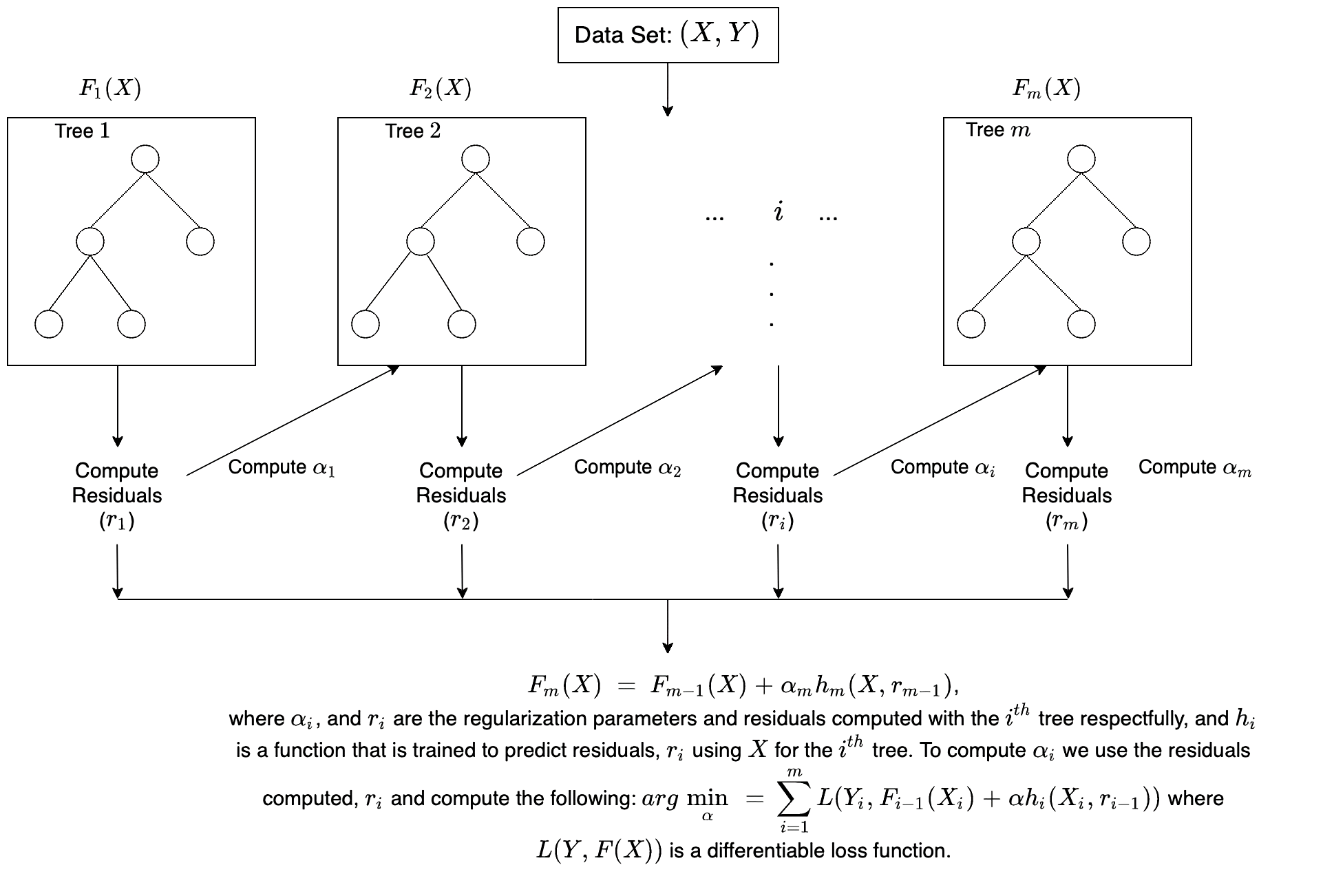
四、随机森林(Random Forest)
1、Bagging
Bagging, also known as Bootstrap aggregating, is an ensemble learning technique that helps to improve the performance and accuracy of machine learning algorithms. It is used to deal with bias-variance trade-offs and reduces the variance of a prediction model. Bagging avoids overfitting of data and is used for both regression and classification models, specifically for decision tree algorithms.
2、随机森林
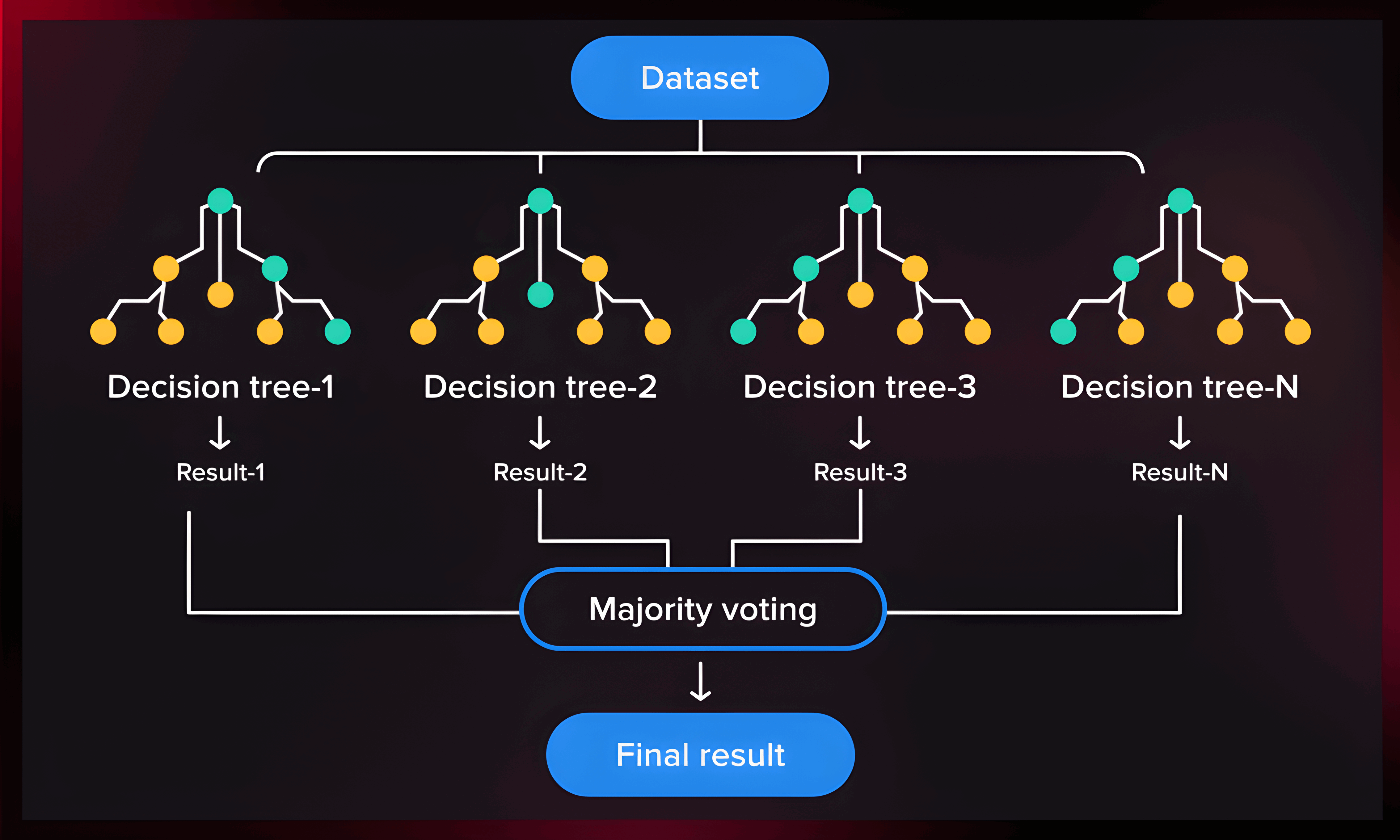
Random forest is a technique used in modeling predictions and behavior analysis and is built on decision trees. It contains many decision trees representing a distinct instance of the classification of data input into the random forest. The random forest technique considers the instances individually, taking the one with the majority of votes as the selected prediction.