一、 监督学习与无监督学习

regression_classification_clustering.png

1、 监督学习（Supervised Learning）

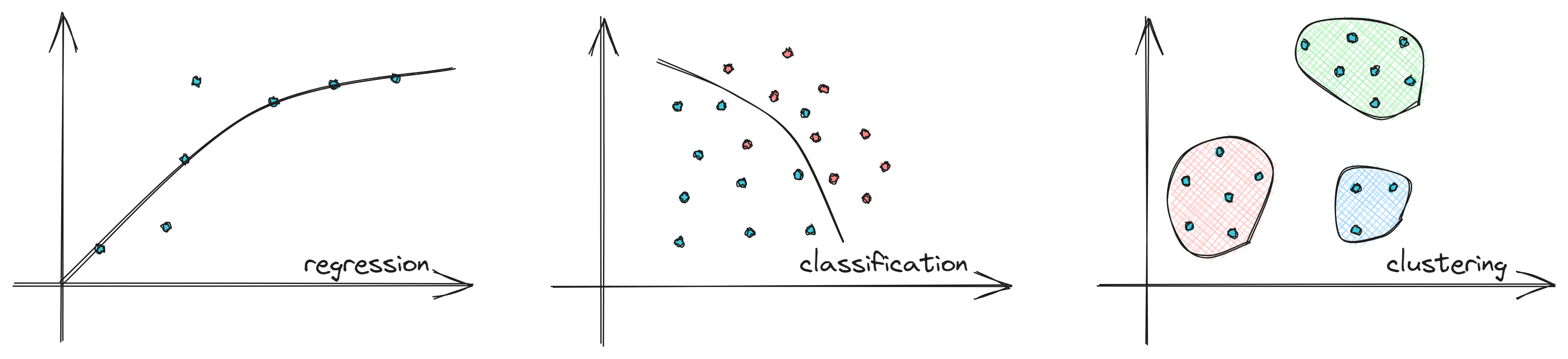
监督学习是指通过让机器学习大量带有标签的样本数据，训练出一个模型，并使该模型可以根据输入得到相应输出的过程。通过已有的一部分输入数据与输出数据之间的对应关系，生成一个函数，将输入映射到合适的输出，例如分类。

回归（Regression）

对于包含房地产的数据集，每行包含具体房屋的相关信息，例如卧室的数量、房屋的大小、卫生间的数量、房屋的价格等。在这个数据集中，房屋价格是每一行的标签。请注意，房屋可能的价格范围太大，无法很好地适应下拉列表。房地产数据集涉及的是回归任务：目标是基于训练模型，然后预测测试数据集中的每个房屋价格。

分类（Classification）

通常用于分类的数据集具有小范围的可能值：如0到9范围内的十个数字之一，四种动物（猫、狗、牛、马）之一，两个值（幸存或已离世、已购买或未购买）之一。根据经验，如果可以在一个下拉列表中以相对较少（主观数目）的值显示结果，则可能是分类任务。

2、无监督学习（Unsupervised Learning）

无监督学习是机器学习中的一种训练方式/学习方式。更像是让机器自学，是没有标签的一种学习。无法清楚判断数据集中数据、特征之间的关系，而是要根据聚类或一定的模型得到数据之间的关系。

聚类（Clustering）

聚类是将相似数据分组在一起的无监督学习技术。聚类算法将数据样本放在不同的集群中，并且不需要了解数据样本的性质。

二、回归模型

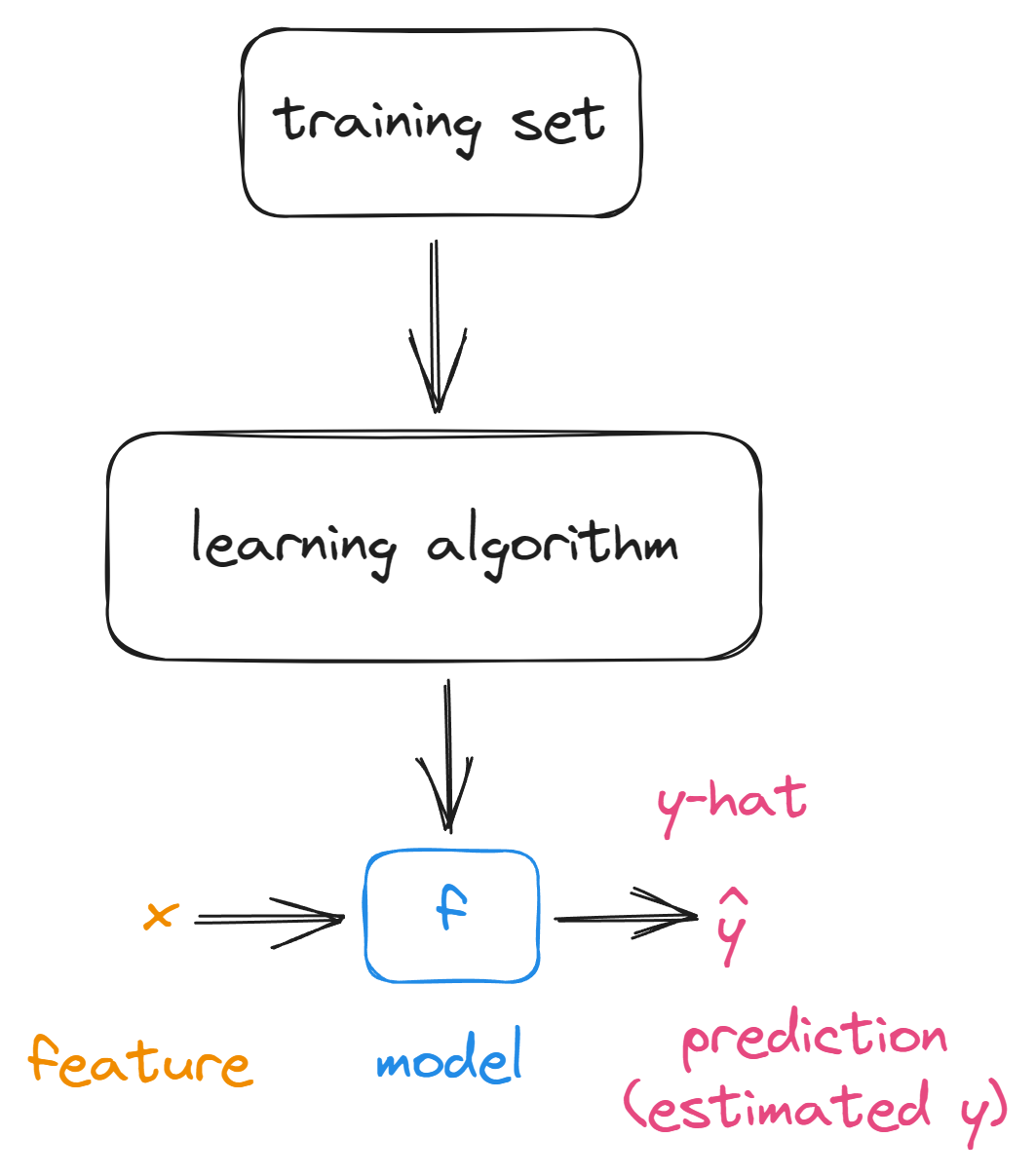
训练集（Training Set）

特征/输入特征（x="input" variable，feature）

目标变量（y="output" variable ，"target" variable）

训练样本（m=number of training examples）

(x,y)=single training example

(x(i),y(i))=ith training example

fw,b(x)=wx+b，w,b：parameters or coefficient or weight

model_training_method.png

1、线性回归（Linear Regression）

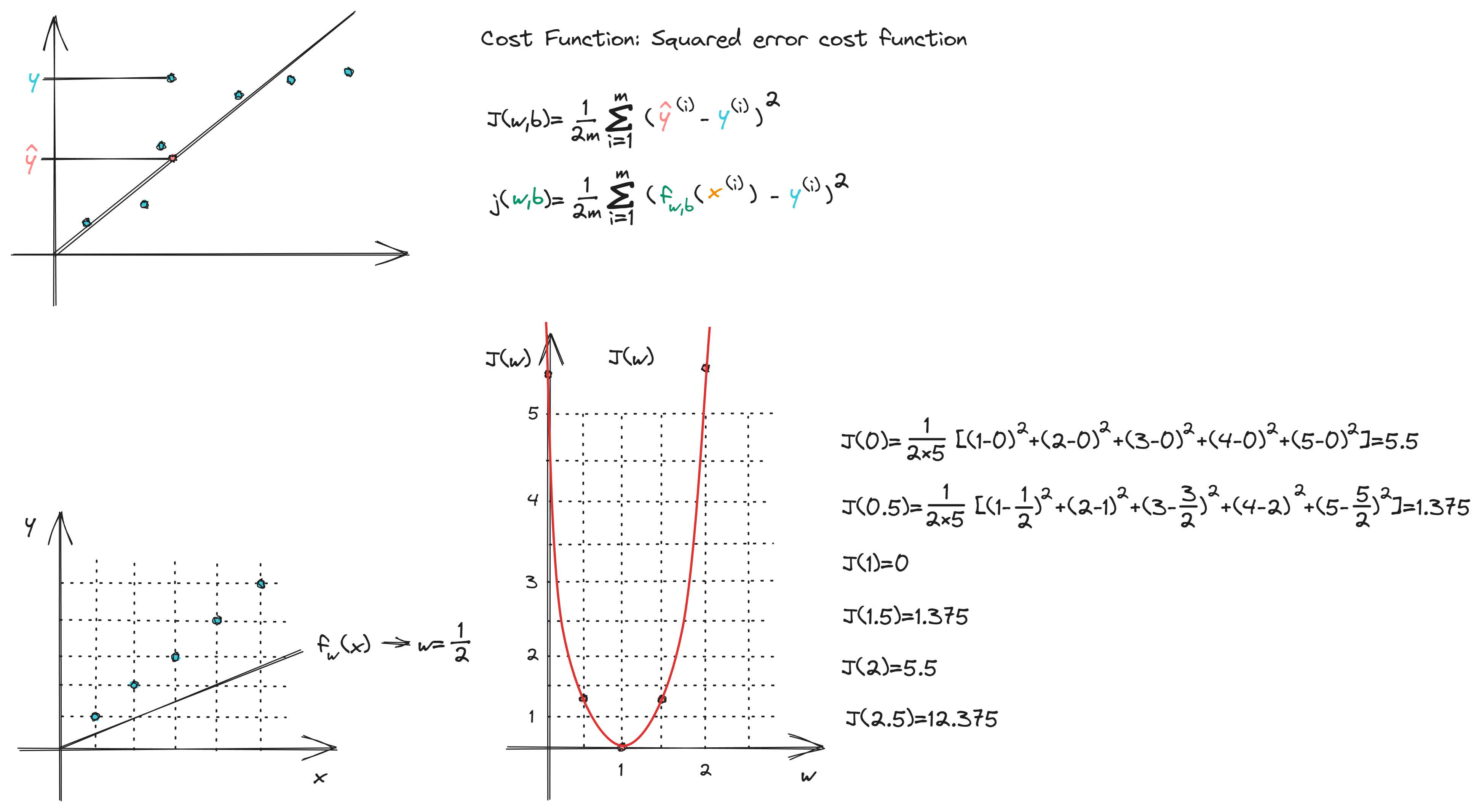
线性回归的目标是找到的参数w或w和b，使得$f_{w,b}(x^{(i)})=wx^{(i)}+b$所在的代价函数J的值最小

损失函数（Cost Function）

对每个y-hat即预测值与实际值的y轴坐标差的平方求和，并且为了缩小其值和求导后方便计算而除2m

$$J(w,b)=\frac{1}{2m} \sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})^2$$

cost_function_graph.png

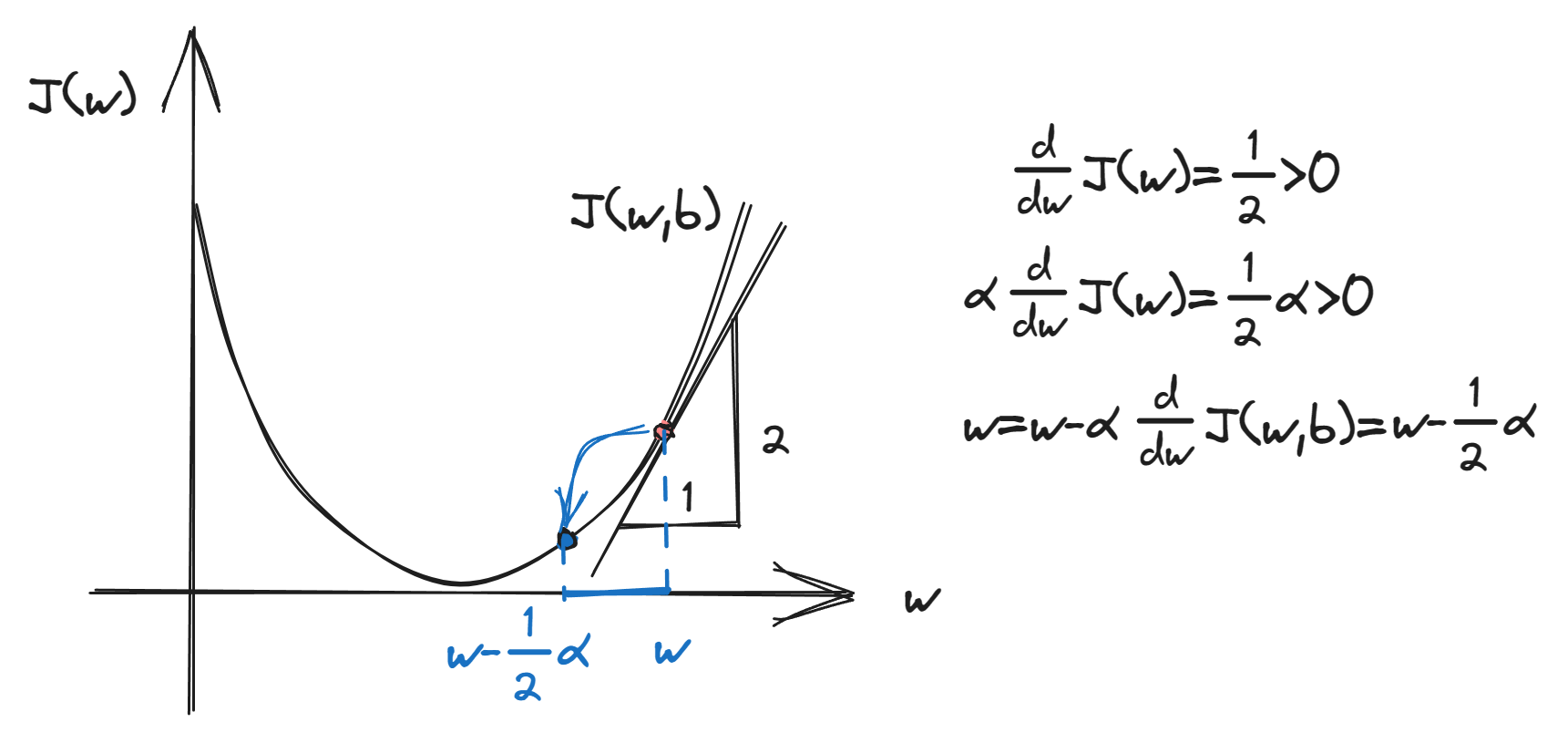
梯度下降（Gradient Descent）

梯度下降算法（其中$\alpha$是学习率，$w,b$需要同时更新，求导时注意是对$w$和$b$求即可）：$\begin{cases}w=w-\alpha\frac{\partial}{\partial w} J(w,b)\to\frac{\partial}{\partial w} J(w,b)=\frac{1}{m}\displaystyle\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)} \\b=b-\alpha\frac{\partial}{\partial b} J(w,b)\to\frac{\partial}{\partial b} J(w,b)=\frac{1}{m}\displaystyle\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)}) \end{cases}$

gradient_descent.png

2、多元线性回归

向量化

使用不同方式计算$ \vec{w} \cdot \vec{d} $

# 100000个数的数组点乘for循环使用了17秒，而numpy的点乘1秒不到
import numpy as np
from datetime import datetime

w = np.random.randint(1, 1000, 100000000)
d = np.random.randint(1, 1000, 100000000)

time_start = datetime.now()
np.dot(w, d)
time_end = datetime.now()
print("np.dot use time: \t", 'start = ', time_start, ' end = ', time_end)

time_start = datetime.now()
for i in range(len(w)):
    arr3 = w[i] + d[i]
time_end = datetime.now()
print("for use time: \t\t", 'start = ', time_start, ' end = ', time_end)

''' 输出：
np.dot use time: 	 start =  2023-06-23 09:29:42.052042  end =  2023-06-23 09:29:42.098940
for use time: 		 start =  2023-06-23 09:29:42.098940  end =  2023-06-23 09:29:59.749573
'''

梯度下降（Gradient Descent）

$$\begin{array}{c}w_1 = w_1-\alpha\frac{1}{m}\displaystyle\sum_{i = 1}^{m}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})x_1^{(i)}\\\vdots\\w_n = w_n-\alpha\frac{1}{m}\displaystyle\sum_{i = 1}^{m}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})x_n^{(i)}\\b=b-\alpha\frac{1}{m}\displaystyle\sum_{i=1}^{m}(f_{\vec{w},b}(x^{(i)})-y^{(i)})\end{array}$$

特征缩放（Feature Scaling）

特征缩放是将不同特征的值量化到同一区间的方法，也是预处理中容易忽视的关键步骤之一。 除了极少数算法（如决策树和随机森林）之外，大部分机器学习和优化算法采用特征缩放后会表现更优。

方式一：$x_{i,scaled}=\frac{x_i}{x_{max}}$

方式二（$\mu$为均值）：$x_{i}=\frac{x_i-\mu_{i}}{x_{max}-x_{min}}$

方式三（正规方程，Z-score normalization，$\sigma$为标准差）：$x_{i}=\frac{x_i-\mu_{i}}{\sigma_i}$

多项式回归（Polynomial regression）

$$f_{\vec{w},b}(x)=w_1x+w_2x^2+w_3x^3+\cdots+w_nx^n$$

3、逻辑回归（Logistic regression）

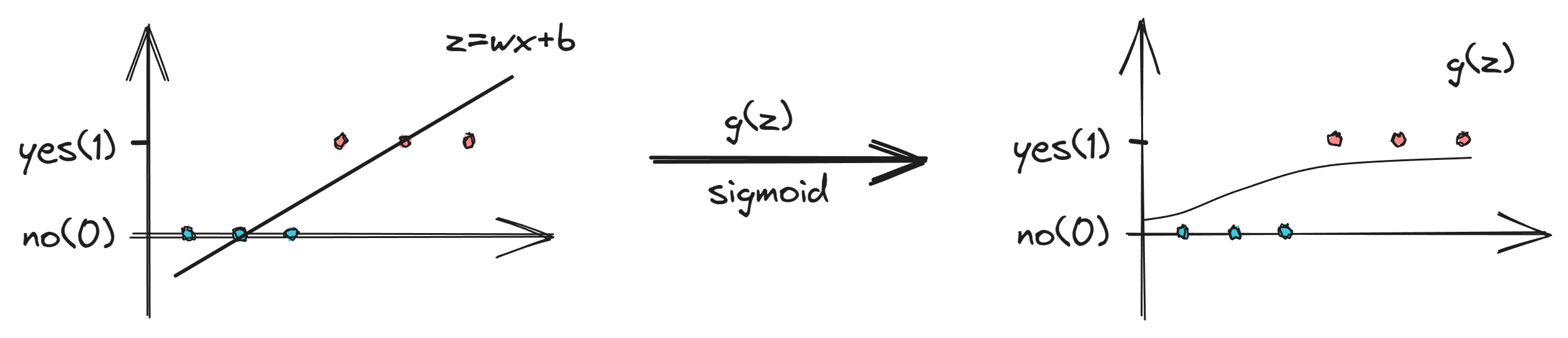
logistic_regression.png

$$f_{\vec{w},b}(\vec{x})=\frac{1}{1+e^{-(\vec{w}\cdot\vec{x}+b)}}$$

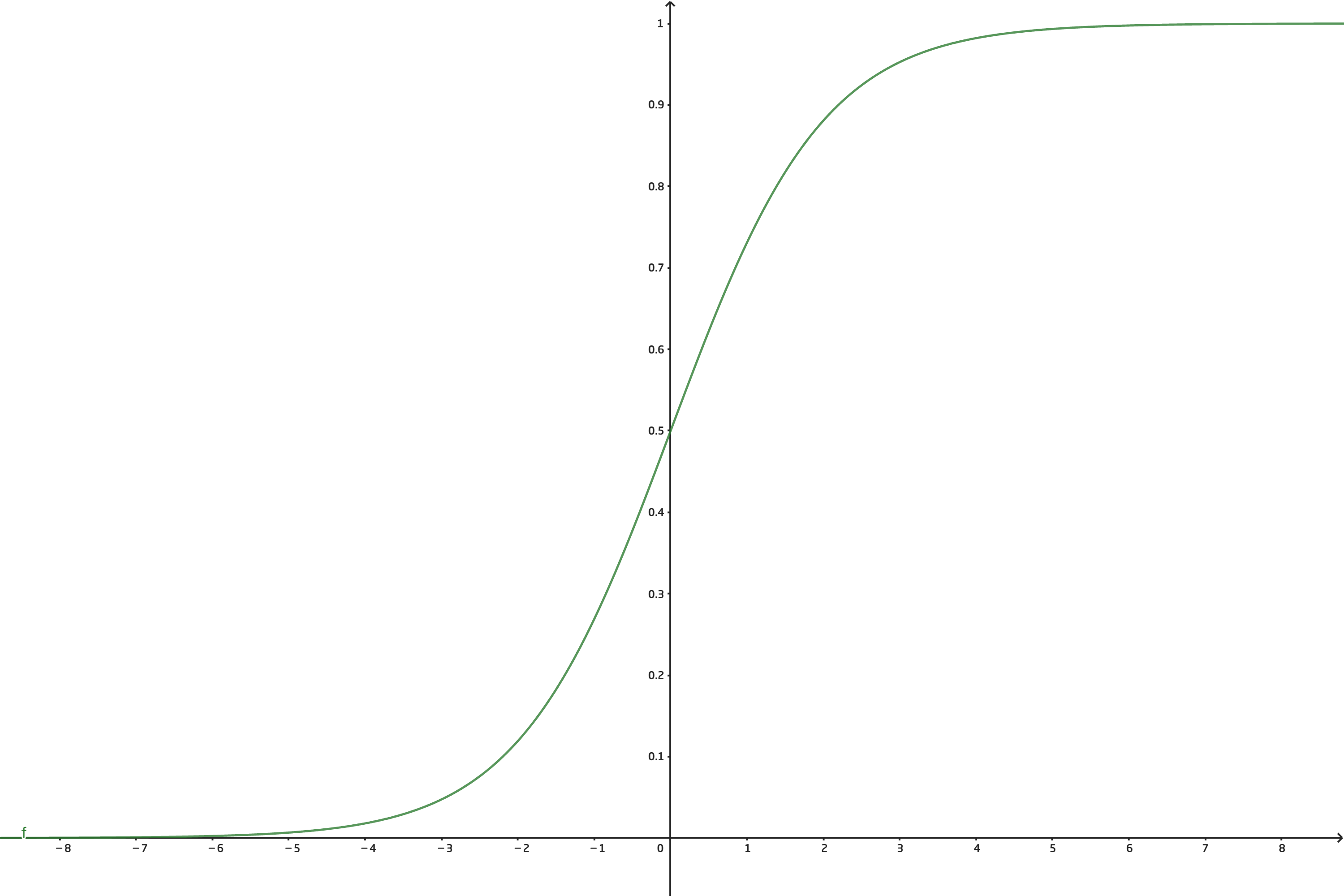
Sigmoid函数

$$g(z)=\frac{1}{1+e^{-z}}$$

sigmoid_function.png

损失函数（Cost Function）

$$\begin{array}{l}J(\vec{w},b)&=\frac{1}{m}\displaystyle \sum_{i=1}^mL(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)}))\\&=-\frac{1}{m}\displaystyle \sum_{i=1}^{m} [y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))+(1-y^{(i)})log(f_{\vec{w},b}(1-\vec{x}^{(i)}))]\end{array}$$

其中$\begin{array}{c}L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)}))=\left\{\begin{matrix}-log(f_{\vec{w},b}(x^{(i)}))\qquad y^{(i)}=1\\-log(1-f_{\vec{w},b}(x^{(i)}))\qquad y^{(i)}=0\end{matrix}\right.\end{array}$

简化后：$L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)}))=-y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))-(1-y^{(i)})log(f_{\vec{w},b}(1-\vec{x}^{(i)}))$

梯度下降（Gradient Descent）

$$\begin{cases}w_j=w_j-\alpha\frac{\partial}{\partial w_j} J(\vec{w},b)\\b=b-\alpha\frac{\partial}{\partial b} J(\vec{w},b)\end{cases}$$

三、过拟合和正则化

1、欠拟合与过拟合

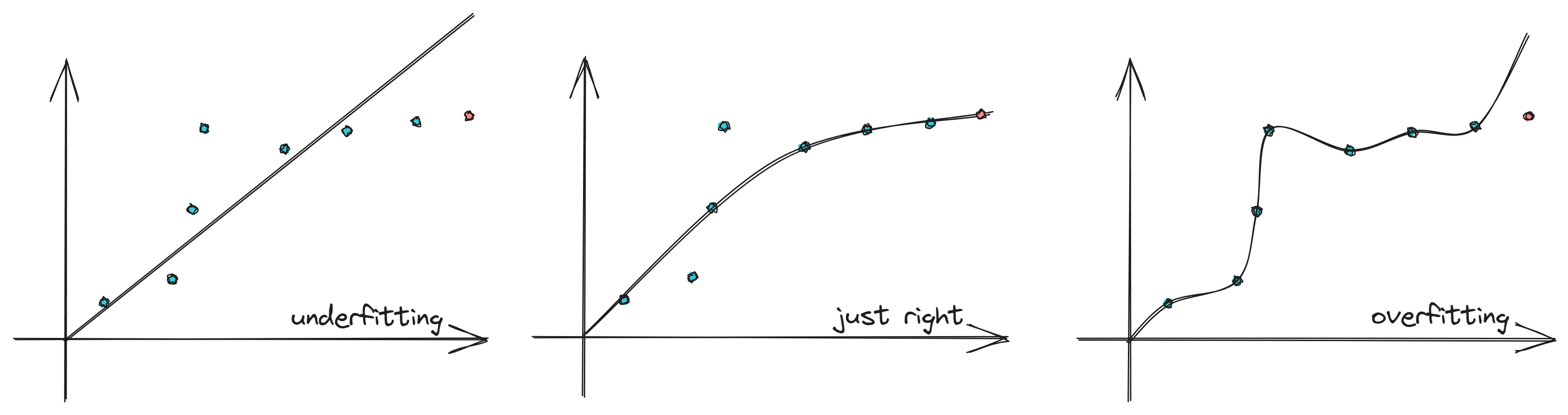underfitting_and_overfitting.png解决过拟合

  • 收集更多数据（Collect more data）

  • 选择并使用特征子集（Select features - Feature selection）

  • 利用正则化减少参数的大小（Reduce size of parameters - "Regularization"）

2、正则化

$$\mathop{min}_{\vec{w},b}J(\vec{w},b)=\mathop{min}_{\vec{w},b}[\frac{1}{2m} \displaystyle\sum_{i=1}^m (f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})^2+\frac{\lambda}{2m}\displaystyle\sum_{j=1}^nw^2_j]$$