一、支持向量机(SVM,Support Vector Machines)
Support Vector Machines (SVMs) are a type of supervised learning algorithm that can be used for classification or regression tasks. The main idea behind SVMs is to find a hyperplane that maximally separates the different classes in the training data. This is done by finding the hyperplane that has the largest margin, which is defined as the distance between the hyperplane and the closest data points from each class. Once the hyperplane is determined, new data can be classified by determining on which side of the hyperplane it falls. SVMs are particularly useful when the data has many features, and/or when there is a clear margin of separation in the data.
二、基本概念
1、决策边界
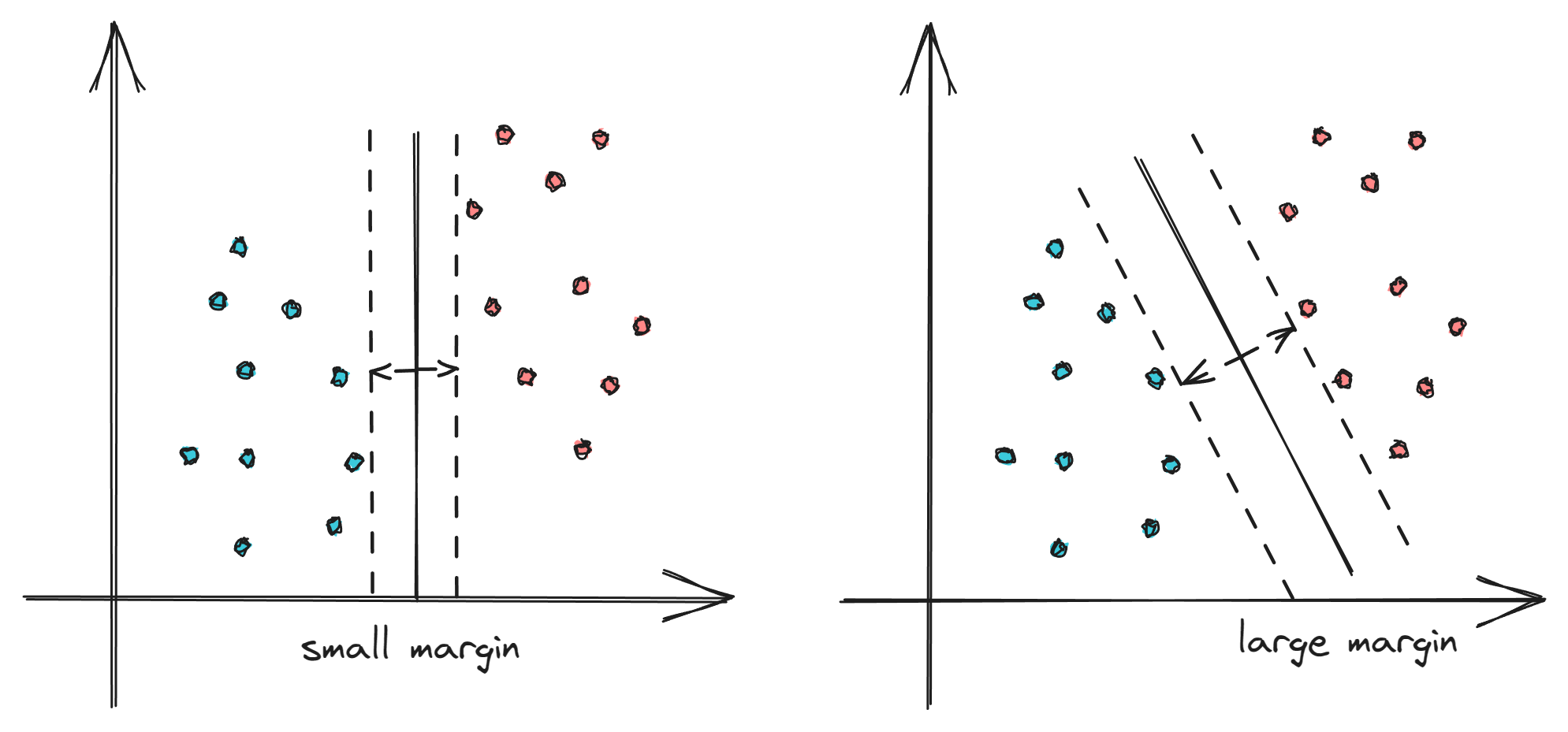
2、点到平面距离的计算
考虑在超平面上有$\boldsymbol x,\boldsymbol x'$使得
$\omega^\mathsf{T}x'=-b,\omega^\mathsf{T}x''=-b$
$\omega^\mathsf{T}\;\bot\;hyperplace:\;\omega^\mathsf{T}(x''-x')=0$
$distance=project(x-x')\;to\;\bot\;hyperplace$
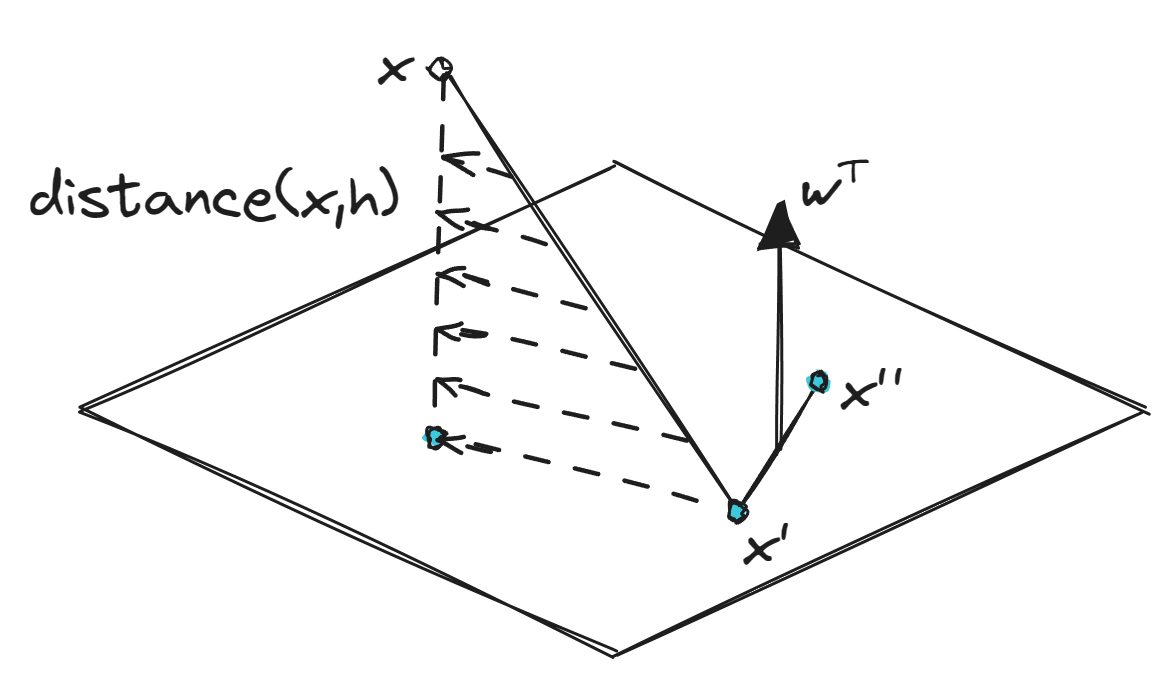
$$distance(\boldsymbol x,b,\boldsymbol \omega)=\bigg|\frac{\boldsymbol \omega^\mathsf{T}}{\mid\mid \boldsymbol \omega\mid\mid}(\boldsymbol x-\boldsymbol x')\bigg|=\frac{1}{\mid\mid \boldsymbol \omega\mid\mid}\mid \boldsymbol \omega^\mathsf{T}\boldsymbol x+b\mid$$
3、数据标签定义
决策方程:$f(x_i)=\omega^\mathsf{T}x_i+b$
给定训练数据$(x_i,y_i)$,其中$i=1\cdots N,x_i\in \mathbb R^d,y_i\in \{-1,1\}$。学习一个分类器$f(x)$使得
$$f(x_i)=\left\{\begin{matrix} \geq 0 & y_i=+1\\ < 0 & y_i=-1 \end{matrix}\right.$$
也就是$y_i\cdot f(x_i)>0$,以便获得正确的分类
4、优化目标
找到一条线($w$和$b$),使得该线与各点的距离最远
点到直线距离化简
$$distance=\frac{y_i\cdot(\omega^\mathsf{T}\cdot x_i+b)}{\mid\mid \omega\mid\mid}$$
优化目标
将$\displaystyle\mathop{arg\;max}_{\omega,b}\bigg\{\frac{1}{\mid\mid \omega\mid\mid}\displaystyle\mathop{min}_{i}[y_i\cdot (\omega^\mathsf{T}\cdot x_i+b)]\bigg\}$,通过放缩变换使$y_i\cdot f(x_i)\ge1$,便只需要考虑$\displaystyle\mathop{arg\;max}_{\omega,b}\frac{1}{\mid\mid \omega\mid\mid}$
常规套路
将求解极大值问题转换成极小值问题:$\displaystyle\mathop{arg\;max}_{\omega,b}\frac{1}{\mid\mid \omega\mid\mid}\Rightarrow \displaystyle\mathop{min}_{\omega,b}\frac12{\mid\mid \omega\mid\mid}^2$
上述问题即在约束条件:$y_i\cdot f(x_i)\ge1\;(i=1\cdots m)$的条件下求$\frac12{\mid\mid \omega\mid\mid}^2$的极小值
5、拉格朗日乘数法
约束条件为等式
目标函数$z=f(x)$在约束条件$\varphi(x)=0$下的极值
令$L(x,\lambda)=f(x)+\lambda\varphi(x)\Rightarrow \left\{\begin{matrix}\frac{\partial L}{\partial x}=0 \\\frac{\partial L}{\partial \lambda}=0\end{matrix}\right.\Rightarrow (x,f(x))$为极值点
KKT条件
摘自文章《KKT条件,原来如此简单 | 理论+算例实践》——科研小飞
$$\begin{matrix}min f(X)\\s.t.\;g(X)\le 0\end{matrix} \Rightarrow \left\{\begin{align*}&\nabla f(X^*)+\lambda\nabla g(X^*)&\quad(1)\\&\lambda g(X^*) = 0&\quad(2)\\&\lambda \ge 0&\quad(3)\\&g(X^*)\le 0&\quad(4)\\\end{align*}\right.$$
(1)对拉格朗日函数求梯度(若X一维就是求导),其中,$\nabla$表示梯度
(2)核心公式,要么λ=0,要么g(X*)=0(此处要求两者不能同时为0)
(3)拉格朗日乘子λ必须是正的
(4)原问题自己的约束
考虑的最优化问题为:$\begin{align*}min\; &f(X)\\s.t.\;&g_i(X)\le 0,\;i = 1,\cdots,m\Rightarrow m个不等式约束\\&h_j(x) = 0,\;j = 1,\cdots,n\Rightarrow n个等式约束\\\end{align*}$
此时定义的拉格朗日函数为:$L(X,\{\lambda_i\},\{\mu_j\})=f(X)+\displaystyle\sum_{i=1}^{m}\lambda_ig_i(X)+\displaystyle\sum_{j=1}^{n}\mu_jh_j(X)$
对应的KKT条件:
$\begin{align*}&\nabla f(X^*)+\displaystyle\sum_{i=1}^{m}\lambda_i\nabla g_i(X)+\displaystyle\sum_{j=1}^{n}\mu_j\nabla h_j(X)=0\quad &(1)\\&\lambda_ig_i(X^*)=0\;i=1,\cdots,m\quad &(2)\\&h_j(X^*),\;j=1,\cdots,n\quad &(3)\\&\lambda_i \ge 0,\;i=1,\cdots,m\quad &(4)\\&g_i \le 0,\;i=1,\cdots,m\quad &(5)\end{align*}$
约束条件为不等式(化为等式)
$L(x,\alpha,\beta)=f(x)+\displaystyle\sum_{i=1}^{m}\alpha_ig_i(x)+\displaystyle\sum_{j=1}^{n}\beta_jh_j(x),\;\alpha_i\ge0$
对偶问题
强对偶条件:
原问题为凸函数
$g_i(x)\quad s.t.\;a_ix+b_i$是线性约束
满足KKT条件
则原问题的解和对偶问题的解相同:$\displaystyle\mathop{min}_{x}\displaystyle\mathop{max}_{\alpha,\beta}L(x,\alpha,\beta)=\displaystyle\mathop{max}_{\alpha,\beta}\displaystyle\mathop{min}_{x}L(x,\alpha,\beta)$
三、公式推导
$f(\omega)=min\frac12\mid\mid\omega \mid\mid^2\quad s.t.\;y_i(\omega^\mathsf{T}x_i+b)\ge 1,\;(i = 1,\cdots,m)$
$g_i(x)=1-y_i(\omega^\mathsf{T}x_i+b)\le 0),\;(i = 1,\cdots,m)$
由$L(x,\alpha,\beta)=f(x)+\displaystyle\sum_{i=1}^{m}\alpha_ig_i(x)+\displaystyle\sum_{j=1}^{n}\beta_jh_j(x)$可知:
$L(\omega,b,\alpha)=\frac12\mid\mid\omega\mid\mid^2+\displaystyle\sum_{i=1}^m\alpha_i(1-y_i(\omega^\mathsf{T}x_i+b))\qquad\alpha_i\ge0(i=1,\cdots,m)$
转换为对偶问题求解:
$\frac{\partial L}{\partial \omega }=\omega -\displaystyle \sum_{i=1}^{m}a_iy_ix_i=0\Rightarrow \omega =\displaystyle \sum_{i=1}^{m}a_iy_ix_i\qquad\frac{\partial L}{\partial b}=\displaystyle \sum_{i=1}^{m}a_iy_i=0$
$\begin{align}L(w,b,\alpha) & = \frac12\mid\mid\omega\mid\mid^2+\displaystyle\sum_{i = 1}^m\alpha_i(1-y_i(\omega^\mathsf{T}x_i+b))\\ &= \frac{1}{2}(\displaystyle\sum_{i = 1}^{m}\alpha_iy_ix_i)^\mathsf{T} (\displaystyle\sum_{i = 1}^{m}\alpha_iy_ix_i)+\displaystyle\sum_{i = 1}^{m}\alpha_i-\displaystyle\sum_{i = 1}^{m}\alpha_iy_i(\displaystyle\sum_{i = 1}^{m}\alpha_iy_ix_i)^\mathsf{T}x_i-\displaystyle\sum_{i = 1}^{m}\alpha_iy_ib\\&=\displaystyle\sum_{i=1}^{m}\alpha_i-\frac12(\displaystyle\sum_{i=1}^{m}\alpha_iy_ix_i)^\mathsf{T}\displaystyle\sum_{i=1}^{m}\alpha_iy_ix_i\\&=\displaystyle\sum_{i=1}^{m}\alpha_i-\frac12\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_ix_j\end{align}$
即求$max\;\displaystyle\sum_{i=1}^{m}\alpha_i-\frac12\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_ix_j\quad$约束条件:$\displaystyle\sum_{i=1}^{m}\alpha_iy_i=0,\;\alpha_i\ge0$
转换为求极小值:$\begin{align}min\;\frac12\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_ix_j-\displaystyle\sum_{i=1}^{m}\alpha_i\quad\end{align}$约束条件:$\displaystyle\sum_{i=1}^{m}\alpha_iy_i=0,\;\alpha_i\ge0$
四、SVM求解实例
数据:三个点,其中正例$x_1(3,3)$,$x_2(4,3)$,负例$x_3(1,1)$,则$y_1=y_2=1$,$y_3=-1$
求解:$\begin{align}\frac12\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\displaystyle\sum_{i=1}^{m}\alpha_i\quad\end{align}$约束条件:$\displaystyle\sum_{i=1}^{3}\alpha_iy_i=\alpha_1+\alpha_2-\alpha_3=0\\\alpha_i\ge0,\;i=1,2,3$
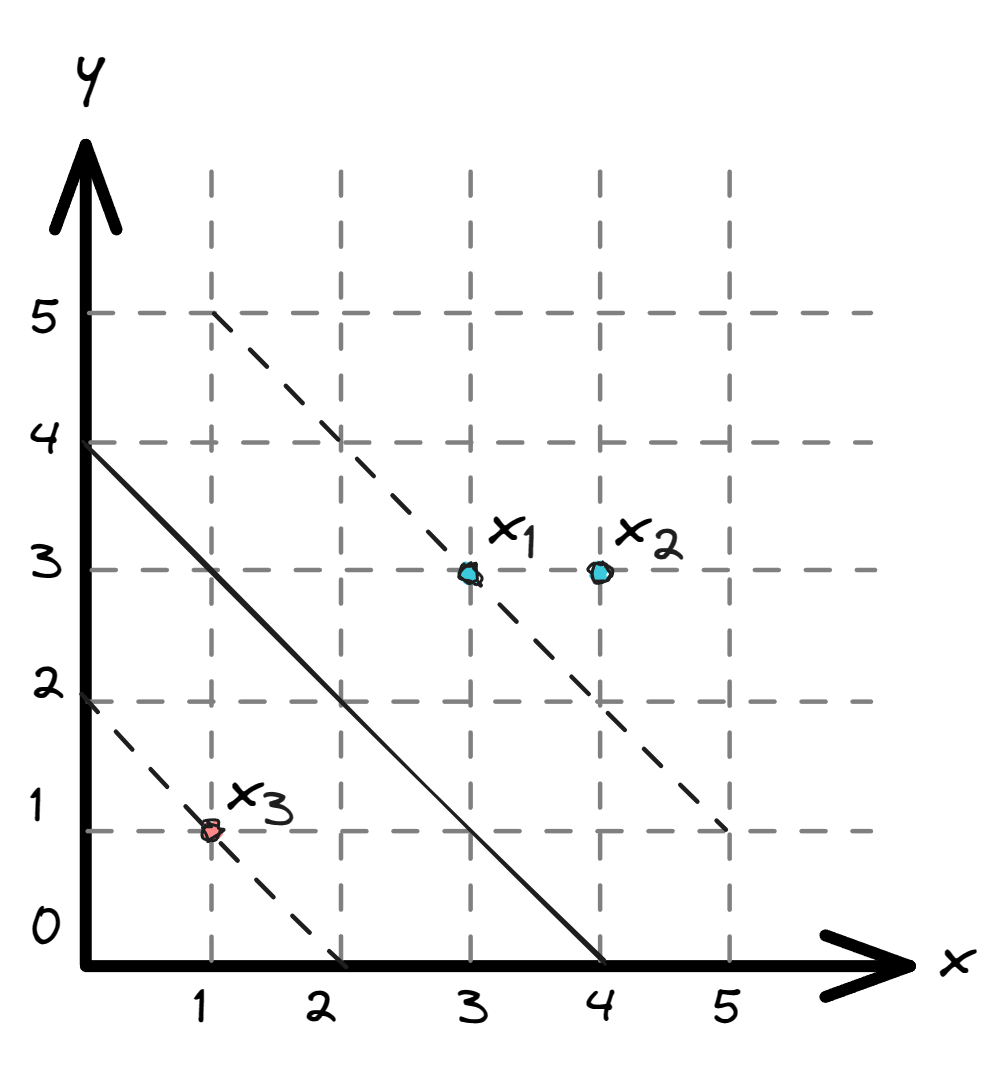
数据:
$\alpha_1+\alpha_2=\alpha_3$
$y_1^2=y_2^2=y_3^2=y_1y_2=1\\y_1y_3=y_2y_3=-1$
$x_1\cdot x_1=(3,3)\cdot(3,3)=18\\x_2\cdot x_2=(4,3)\cdot(4,3)=25\\x_3\cdot x_3=(1,1)\cdot(1,1)=2\\x_1\cdot x_2=x_2\cdot x_1=(3,3)\cdot(4,3)=21\\x_1\cdot x_3=x_3\cdot x_1=(3,3)\cdot(1,1)=6\\x_2\cdot x_3=x_3\cdot x_2=(4,3)\cdot(1,1)=7$
将数据带入:
$\begin{align}L(w,b,\alpha) &=\frac12\displaystyle\sum_{i=1}^3\displaystyle\sum_{j=1}^3\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\displaystyle\sum_{i=1}^{3}\alpha_i\quad\\&=\frac12(a_1^2y_1^2(x_1\cdot x_1)+a_2^2y_2^2(x_2\cdot x_2)+a_3^2y_3^2(x_3\cdot x_3)\\&\quad+2a_1a_2y_1y_2(x_1\cdot x_2)+2a_1a_3y_1y_3(x_1\cdot x_3)+2a_2a_3y_2y_3(x_2\cdot x_3))\\&\quad-a_1-a_2-a_3\\&=\frac12(18a_1^2+25a_2^2+2a_3^2+42a_1a_2-12a_1a_3-14a_2a_3)-a_1-a_2-a_3\\&=4a_1^2+\frac{13}{2}a_2^2+10a_1a_2-2a_1-2a_2\end{align}$
分别对$\alpha_1,\alpha_2$求偏导,偏导等于0可得:$\begin{align}\alpha_1=1.5\\\alpha_2=-1\end{align}$(不满足约束条件$\alpha_i\ge 0$所以解应该在边界上)
$\left\{\begin{matrix}\alpha_1=0\Rightarrow\alpha_2=\frac{2}{13}\Rightarrow L_1=-\frac{2}{13}\\\alpha_2=0\Rightarrow\alpha_1=\frac14\Rightarrow L_2=-\frac14\end{matrix}\right.$($L_2<L_1$,则其为最小值,故最小值在$(\frac14,0,\frac14)$处取得)
将结果带入求解:
$\omega =\displaystyle \sum_{i=1}^{m}a_iy_ix_i=\frac14\cdot 1\cdot(3,3)+\frac14\cdot-1\cdot(1,1)=(\frac12,\frac12)$
$f(x_j)=\omega x_j+b=(\displaystyle\sum_{i=1}^3a_iy_ix_i)\cdot x_j+b\\\Rightarrow f(x_1)=a_1y_1(x_1\cdot x_1)+a_3y_3(x_3\cdot x_1)+b\\\quad=(\frac14\cdot1\cdot18+\frac14\cdot -1\cdot6)+b=1\\\Rightarrow b=-2$
平面方程:$\frac12x_1+\frac12x_2-2=0$
五、软间隔
松弛因子:$y_i(\omega\cdot x_i+b)\ge1-\xi_i$
新的目标函数:$min\;\frac12\mid\mid w\mid\mid^2+C\displaystyle\sum_{i=1}^{m}\xi_i$
拉格朗日乘数法:$L(\omega,b,\alpha)=\frac12\mid\mid\omega\mid\mid^2+\displaystyle\sum_{i=1}^m\alpha_i(1-y_i(\omega^\mathsf{T}x_i+b))+C\displaystyle\sum_{i=1}^{m}\xi_i-\displaystyle\sum_{i=1}^{m}\mu_i\xi_i$
约束:$\begin{align}&\omega =\displaystyle \sum_{i=1}^{m}a_iy_ix_i\\&\displaystyle \sum_{i=1}^{m}a_iy_i=0\\&C-\alpha_i-\mu_i=0\\&\alpha_i\ge0\quad\mu_i\ge0\end{align}$$\qquad$同样的解法:$\begin{align}&\mathop{min}_{\alpha}\frac12\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\displaystyle\sum_{i=1}^{m}\alpha_i\\&\displaystyle\sum_{i=1}^{m}\alpha_iy_i=0\\&0\le\alpha_i\le C\end{align}$
六、序列最小优化算法(SMO)
$\begin{align}L=\frac12\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\displaystyle\sum_{i=1}^{m}\alpha_i\end{align}$
$\require{cancel}\displaystyle\sum_{i = 1}^m\displaystyle\sum_{j = 1}^m\xrightarrow[去重]{展开}\left\{\begin{matrix} i = 1,\quad j = 1\\ i = 1,\quad j = 2\\ i = 1,\quad j\ge3\\ i = 2,\quad j = 1\\ i = 2,\quad j = 2\\ i = 2,\quad j\ge3\\ \cancel{j = 1,\quad i = 1}\\ \cancel{j = 1,\quad i = 2}\\ j = 1,\quad i\ge3\\ \cancel{j = 2,\quad i = 1}\\ \cancel{j = 2,\quad i = 2}\\ j = 2,\quad i\ge3\\ i\ge3,\quad j\ge3\end{matrix}\right.\xrightarrow{合并同类项} \left\{\begin{array}{l} i = 1,\quad j = 1\\ (i = 1,\quad j = 2) = (i = 2,\quad j = 1)\\ i = 2,\quad j = 2 \\ (i = 1,\quad j\ge3) = (j = 1,\quad i\ge3)\\ (i = 2,\quad j\ge3) = (j = 2,\quad i\ge3)\\ i\ge3,\quad j\ge3\end{array}\right.$
$\begin{align}L(\alpha_1,\alpha_2) & =\frac12\bigg[\alpha_1^2(x_1\cdot x_1)+2\alpha_1\alpha_2y_1y_2(x_1\cdot x_2)+\alpha_2^2(x_2\cdot x_2)\\&\quad+2\displaystyle\sum_{i=3}^{m}\alpha_1\alpha_iy_1y_i(x_1\cdot x_i)+2\displaystyle\sum_{i=3}^{m}\alpha_2\alpha_iy_2y_i(x_2\cdot x_i)+\displaystyle\sum_{i=3}^m\displaystyle\sum_{j=3}^m\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)\bigg]\\& \quad-(\alpha_1+\alpha_2+\displaystyle\sum_{i=3}^{m}\alpha_i)\end{align}$
其中$\displaystyle\sum_{i=3}^m\displaystyle\sum_{j=3}^m\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)$和$\displaystyle\sum_{i=3}^{m}\alpha_i$可视为常数,不影响后续求导,故不在参与后续计算
令$K_{ij}=(x_i\cdot x_j)$
$\begin{align}L(\alpha_1,\alpha_2) & =\frac12\bigg( \alpha_1^2K_{11}+2\alpha_1\alpha_2y_1y_2K_{12}+\alpha_2^2K_{22}\\&\quad+2\displaystyle\sum_{i=3}^{m}\alpha_1\alpha_iy_1y_iK_{1i}+2\displaystyle\sum_{i=3}^{m}\alpha_2\alpha_iy_2y_iK_{2i}\bigg)-\alpha_1-\alpha_2\end{align}$
由约束条件:$\begin{align}\displaystyle\sum_{i=1}^{m}\alpha_iy_i=\alpha_1y_1+\alpha_2y_2+\displaystyle\sum_{i=3}^{m}\alpha_iy_i=0\Rightarrow\alpha_1y_1+\alpha_2y_2=-\displaystyle\sum_{i=3}^{m}\alpha_iy_i=C\end{align}$
可知:$\begin{align}\alpha_1=\frac{C-\alpha_2y_2}{y_1}=y_1(C-\alpha_2y_2)\end{align}$,并带入$L(\alpha_1,\alpha_2)$,并求导数为0的点
$\begin{align}L(\alpha_2)&= \frac12\bigg[ (C-\alpha_2y_2)^2K_{11}+2y_2(C\alpha_2-\alpha_2^2y_2)K_{12}+\alpha_2^2K_{22}\\&\quad+2\displaystyle\sum_{i=3}^{m}(C-\alpha_2y_2)\alpha_iy_iK_{1i}+2\displaystyle\sum_{i=3}^{m}\alpha_2\alpha_iy_2y_iK_{2i}\bigg]-y_1(C-\alpha_2y_2)-\alpha_2 \end{align}$
$\begin{align}\frac{\partial L}{\partial \alpha_2}&= \frac12\bigg[ 2(-y_2)(C-\alpha_2y_2)K_{11}+2y_2(C-2\alpha_2y_2)K_{12}+2\alpha_2K_{22}\\&\quad-2\displaystyle\sum_{i=3}^{m}y_2\alpha_iy_iK_{1i}+2\displaystyle\sum_{i=3}^{m}\alpha_iy_2y_iK_{2i} \bigg]+y_1y_2-1\\&=\alpha_2K_{11}-Cy_2K_{11}+Cy_2K_{12}-2\alpha_2K_{12}+\alpha_2K_{22}\\&\quad-\displaystyle\sum_{i=3}^{m}y_2\alpha_iy_iK_{1i}+\displaystyle\sum_{i=3}^{m}\alpha_iy_2y_iK_{2i}+y_1y_2-1\\&=0\end{align}$
移项:
$\begin{align}\alpha_2(K_{11}+K_{22}-2K_{13})&=Cy_2K_{11}-Cy_2K_{12}+\displaystyle\sum_{i=3}^{m}y_2\alpha_iy_iK_{1i}-\displaystyle\sum_{i=3}^{m}\alpha_iy_2y_iK_{2i}-y_1y_2+1\\&=y_2(CK_{11}-CK_{12}+\displaystyle\sum_{i=3}^{m}\alpha_iy_iK_{1i}-\displaystyle\sum_{i=3}^{m}\alpha_iy_iK_{2i}-y_1+y_2)\end{align}$
由$\omega=\displaystyle\sum_{i=1}^{m}\alpha_iy_ix_i$和$f(x_k)=\omega^\mathsf{T}x_k+b$
$\begin{align}f(x_k)&=\displaystyle\sum_{i=1}^{m}\alpha_iy_ix_i^\mathsf{T}x_k+b=\alpha_1y_1x_1^\mathsf{T}x_k+\alpha_2y_2x_2^\mathsf{T}x_k+\displaystyle\sum_{i=1}^{m}\alpha_iy_ix_i^\mathsf{T}x_k+b\\&=\alpha_1y_1K_{1k}+\alpha_2y_2K_{2k}+\displaystyle\sum_{i=1}^{m}\alpha_iy_iK_{ik}+b\end{align}$
$\begin{align}\displaystyle\sum_{i=1}^{m}\alpha_iy_iK_{ik}=f(x_k)-\alpha_1y_1K_{1k}-\alpha_2y_2K_{2k}-b\end{align}$
可以得出:
$\begin{align}\left\{\begin{array}{l}\displaystyle\sum_{i=1}^{m}\alpha_iy_iK_{1i}=f(x_1)-\alpha_1y_1K_{11}-\alpha_2y_2K_{21}-b\quad &(1)\\\displaystyle\sum_{i=1}^{m}\alpha_iy_iK_{2i}=f(x_2)-\alpha_1y_1K_{12}-\alpha_2y_2K_{22}-b &(2)\\\alpha_1^{old}y_1+\alpha_2^{old}y_2=C\qquad &(3)\end{array}\right.\end{align}$
将$(1),(2),(3)$代入$\begin{array}{l}\alpha^{new,unc}_2(K_{11}+K_{22}-2K_{13})=y_2(CK_{11}-CK_{12}+\displaystyle\sum_{i=3}^{m}\alpha_iy_iK_{1i}-\displaystyle\sum_{i=3}^{m}\alpha_iy_iK_{2i}-y_1+y_2)\\\quad=y_2\bigg[ (\alpha_1^{old}y_1+\alpha_2^{old}y_2)K_{11}-(\alpha_1^{old}y_1+\alpha_2^{old}y_2)K_{12} \\\qquad+f(x_1)-\alpha_1y_1K_{11}-\alpha_2y_2K_{21}-b-f(x_2)+\alpha_1y_1K_{12}+\alpha_2y_2K_{22}+b-y_1+y_2\bigg]\\\quad =y_2\bigg[\displaystyle\mathop{\underline{\alpha^{old}_1y_1K_{11}}}_{A}+\alpha^{old}_2y_2K_{11}\displaystyle\mathop{\underline{-\alpha^{old}_1y_1K_{12}}}_{B}-\alpha^{old}_2y_2K_{12}+f(x_1)\\\qquad\displaystyle\mathop{\underline{-\alpha^{old}_1y_1K_{11}}}_{-A}-\alpha^{old}_2y_2K_{21}\displaystyle\mathop{\underline{-b}}_{C}-f(x_2)\displaystyle\mathop{\underline{+\alpha^{old}_1y_1K_{12}}}_{-B}+\alpha^{old}_2y_2K_{22}\displaystyle\mathop{\underline{+b}}_{-C}-y_1+y_2 \bigg]\\\quad=y_2\bigg[\displaystyle\mathop{\underline{(f(x_1)-y_1)}}_{E_1}-\displaystyle\mathop{\underline{(f(x_2)-y_2)}}_{E_2}+\alpha^{old}_2y_2\displaystyle\mathop{\underline{(K_{11}+K_{22}-2K_{12})}}_{\eta }\bigg]\end{array}$
化简可得:
$\alpha^{new,unc}_2\eta=y_2(E_1-E_2)+\alpha^{old}_2\eta\Rightarrow\alpha^{new,unc}_2=\alpha^{old}_2+\frac{y_2(E_1-E_2)}{\eta}$
$\alpha^{new,unc}_1=y_1(C-\alpha^{new,unc}_2)=y_1(\alpha^{old}_1y_1+\alpha^{old}_2y_2-\alpha^{new,unc}_2y_2)=\alpha^{old}+y_1y_2(\alpha^{old}_2-\alpha^{new,unc}_2)$
最终得到:
$\boxed{\alpha^{new,unc}_2=\alpha^{old}_2+\frac{y_2(E_1-E_2)}{\eta}\\\alpha^{new,unc}_1=\alpha^{old}+y_1y_2(\alpha^{old}_2-\alpha^{new,unc}_2)}$
七、核函数
支持向量机通过某非线性变换$\varphi(x)$,将输入空间映射到高维特征空间
$d_i=\begin{pmatrix} x_1^i\\x_2^i\end{pmatrix}\xrightarrow{\varphi(x)}\varphi(d_i)=\begin{pmatrix} (x_1^i)^2\\\sqrt2x_1^ix_2^i\\(x_2^i)^2\end{pmatrix}$
$d_1=\begin{pmatrix} x_1^1\\x_2^1\end{pmatrix}\xrightarrow{\varphi(x)}\varphi(d_1)=\begin{pmatrix} (x_1^1)^2\\\sqrt2x_1^1x_2^1\\(x_2^1)^2\end{pmatrix}\qquad d_2=\begin{pmatrix} x_1^2\\x_2^2\end{pmatrix}\xrightarrow{\varphi(x)}\varphi(d_2)=\begin{pmatrix} (x_1^2)^2\\\sqrt2x_1^2x_2^2\\(x_2^2)^2\end{pmatrix}$
$\begin{align}\varphi^\mathsf{T}(d_1)\varphi(d_2)&=(x_1^1)^2(x_1^2)^2+2x_1^1x_1^2x_2^1x_2^2+(x_2^1)^2(x_2^2)^2\\(d_1^\mathsf{T}d_2)^2&=(x_1^1)^2(x_1^2)^2+2x_1^1x_1^2x_2^1x_2^2+(x_2^1)^2(x_2^2)^2\end{align}$
通过计算低维的$(d_1,d_2)^2$即可的到升维后的$\varphi^\mathsf{T}(d_1)\varphi(d_2)$
高斯核函数
$$\begin{align}k(x,x')=e^{-\frac{\mid\mid x-x' \mid\mid^2}{2\sigma^2}}\end{align}$$
$\begin{align}k(x,x') & = e^{-\frac{\mid\mid x-x' \mid\mid^2}{2\sigma^2}}\\ & = e^{-\frac{x^2+x'^2-2xx'}{2\sigma^2}}\\ & =\displaystyle\mathop{\underline{e^{\frac{x^2}{2\sigma^2}}\cdot e^{\frac{x'^2}{2\sigma^2}}}}_{K}\cdot e^{\frac{xx'}{2\sigma^2}}\\ &=K\cdot e^{\frac{xx'}{2\sigma^2}} \\ & =K(1+\frac{x}{\sigma}\frac{x'}{\sigma}+\cdots+\frac{(\frac{x}{\sigma})^n}{\sqrt{n}!}\frac{(\frac{x'}{\sigma})^n}{\sqrt{n}!}) \\ & =K\cdot\boxed{\begin{pmatrix} 1 ,\frac{x}{\sigma},\cdots,\frac{(\frac{x}{\sigma})^n}{\sqrt{n}!}\end{pmatrix}\begin{pmatrix} 1\\ \frac{x'}{\sigma}\\\vdots\\\frac{(\frac{x'}{\sigma})^n}{\sqrt{n}!}\end{pmatrix}}无限维\end{align}$
$\begin{align}d=\mid\mid \varphi(x)-\varphi(x’)\mid\mid^2&= \varphi^\mathsf{T}(x) \varphi(x)-2 \varphi^\mathsf{T}(x) \varphi^\mathsf{T}(x')+ \varphi(x') \varphi(x')\\&=2-2e^{\frac{\mid\mid x-x'\mid\mid^2}{2\sigma^2}}\end{align}$
$\sigma$增大$d$减小,区分度下降;$\sigma$减小$d$增大,区分度提升
